By Por Katia Regina Ashton Nunes
“Por favor toquem nas obras”
“Todo mundo tem, potencialmente, a capacidade de criar. Agora, se ela é condicionada num meio que não favorece, ela acaba não criando”
“Nós somos os propositores: enterramos a obra de arte como tal e chamamos você para que o pensamento viva através de sua ação.”
“A arte não consiste mais em um objeto para você olhar, achar bonito, mas para uma preparação para a vida.”
[Lygia Clark]
Lygia Clark. Crédito: Divulgação/Associação Cultural O Mundo de Lygia Clark.
Uma grande mulher que revolucionou o espaço do museu e as artes plásticas e, que este ano, completaria 100 anos: seu nome é Lygia Pimentel Lins, conhecida por Lygia Clark, artista brasileira admirada no mundo todo e que não pode deixar de ser reverenciada e festejada.
Quando conheci sua obra, abriu-se um leque à minha frente. Ao aprofundar meu conhecimento sobre esta pintora e escultora mineira, pude perceber o quanto suas ideias e trajetória artística, poderiam colaborar para uma transformação de um espaço que conhecia e apreciava: minha sala de aula de Matemática.
Lygia Clark revolucionou o espaço do museu e principalmente a relação espectador-obra de arte. Ela deslocou-se da posição de artista para a de propositora, rompendo assim com a ideia de que a arte devia ser apenas observada, contemplada. Seu desejo era criar uma arte que conciliasse os sentidos da experimentação e da participação. Disse adeus à contemplação passiva; e transformou o espectador em coautor de suas obras. Em suas exposições convidava o espectador a participar ao colocar o aviso: “por favor, toquem as obras”.
Leia mais: Os 100 anos de Loris Malaguzzi. E o desenvolvimento da abordagem Reggio Emilia
Interatividade e participação são palavras-chave nas obras de Lygia Clark. E justamente são essas as palavras que acredito que devem estar presentes em toda sala de aula, e em especial na sala de aula de Matemática.
O professor não pode mais ser apenas um transmissor de conhecimentos, ele precisa ser um mediador. Seu objetivo principal deve ser o de criar condições para que o aluno participe mais ativamente e independentemente na construção do seu próprio conhecimento. Pois, como dizia Lygia Clark, “todo mundo tem, potencialmente, a capacidade de criar. Agora, se ela é condicionada num meio que não favorece, ela acaba não criando”.
Essa instigante artista se tornou propositora e transformou o espectador passivo em participante ativo. Tomando-a como espelho, meu objetivo foi me tornar propositora, mediadora de aprendizagens, e fazer com que meus alunos pudessem sair da posição de meros espectadores e receptores para a de participantes e criadores; transformando o espaço da minha sala de aula de Matemática em um ambiente de pesquisa, de diálogo, de descoberta e de reflexão. Um ambiente onde se pudesse desenvolver a diversidade de pensamento, a sensibilidade, a curiosidade, a imaginação, a criatividade e a criação.
“Nós somos os propositores: enterramos a obra de arte como tal e chamamos você para que o pensamento viva através de sua ação”. [CLARK ]
Para desenvolver minha pesquisa com Matemática e Arte, além de mergulhar nas obras e ideias dessa artista, passei a investigar a função e a importância da Arte e como esta área do conhecimento, poderia colaborar como parceira na busca da transformação da minha sala de aula. Já que:
“conhecer arte envolve o exercício conjunto do pensamento, da intuição, da sensibilidade e da imaginação “ [PCN ARTE ]
“A arte não é apenas básica, mas fundamental na educação de um país que se desenvolve (…). Não é possível uma educação intelectual, formal ou informal, sem a arte, porque é impossível o desenvolvimento integral da inteligência sem o desenvolvimento do pensamento divergente, do pensamento visual e do conhecimento presentacional que caracterizam a arte. Se pretendemos uma educação não apenas intelectual, mas principalmente humanizadora, a necessidade da arte é ainda mais crucial para desenvolver a percepção e a imaginação, para capturar a realidade circundante e desenvolver a capacidade criadora necessárias à modificação desta realidade. [BARBOSA]
“a arte é a transformação do ordinário no extraordinário. E a matemática é a maneira de, através do ordinário, explicar o extraordinário”. [ PETICOV ]
Leia mais: Como aprender matemática, geografia e física ao brincar de pipa
Nos projetos que desenvolvo envolvendo Matemática e Arte, convido, inicialmente, meus alunos a descrever quais as sensações são despertadas ao observar as obras escolhidas. Depois proponho pesquisar o nome da obra, o ano em que ela foi feita, as dimensões, a técnica, os materiais empregados, e um pouco sobre a vida e da obra do artista, procurando caracterizar o contexto histórico, político e social de sua época.
Após essa fase, peço aos alunos que soltem a imaginação e criatividade e façam, individualmente ou coletivamente, suas próprias leituras/ interpretações das obras analisadas, e muitas outras produções/criações. A próxima etapa é a elaboração de estudos, onde são explorados, diversas competências e habilidades e muitos conceitos matemáticos.
Em todos os projetos a História, a Geografia e a Língua Portuguesa são disciplinas que se integram de modo natural ao trabalho, possibilitando assim a criação de um diálogo interdisciplinar permanente.
“aprenderemos mais integrando os conteúdos e as habilidades; a lógica e o afeto; o sensorial, o emocional e o racional; o passado e o presente. Aprendemos melhor quando vivenciamos, experimentamos, sentimos.” [MORAN]
A trajetória de Lygia Clark, uma expoente da arte
Lygia Clark iniciou seus estudos artísticos em 1947, no Rio de Janeiro, sob a orientação de Burle Marx. Do paisagista, herda a necessidade de inserir em seu trabalho questões orgânicas que tiveram importância fundamental no desenvolvimento de sua pesquisa com o espaço. Em 1950, viaja a Paris, onde estuda com Fernand Léger. Nesse período, a artista dedica-se à realização de estudos em telas e óleos.
Escadas- 1951
Após sua primeira exposição individual em Paris, no ano de 1952, a artista retorna ao Rio de Janeiro. Em 1954, passa a integrar o Grupo Frente, núcleo do concretismo carioca, com Hélio Oiticica, Lygia Pape, Aloísio Carvão, Ivan Serpa, entre outros, criado quase concomitantemente à constituição do Grupo Ruptura, que reunia os concretista de São Paulo, liderado por Waldemar Cordeiro e, inicialmente constituído, por Lothar Charroux, Geraldo de Barros, Kazmer Féjer, Leopold Haar,Luís Sacilotto e Anatol Wladyslaw.
A diferença entre esses dois grupos tem sua origem na interpretação teórica e prática que cada um deles fez de sua inserção nas questões internacionais da arte concreta, cuja principal característica era ser uma arte de aspiração universal, que repudiava as referências figurativas, a imitação e representação e baseava-se no uso de formas geométricas simples.
“Defendemos a linguagem real da pintura que se exprime em linhas e cores, que são linhas e cores e não desejam ser nem peras nem homens”. [CORDEIRO]
Unidade tripartida (1948-1949)
A arte concreta tinha como figura central o pintor, escultor, designer e arquiteto suíço Max Bill. Ele foi o responsável por trazer a arte concreta de forma efetiva ao meio de arte brasileiro ao realizar uma grandiosa exposição no Museu de Arte de São Paulo, em 1950, e ao vencer o Grande Prêmio de Escultura na I Bienal Internacional de São Paulo que ocorreu em 1951 com a obra Unidade tripartida.
Max Bill defendia um padrão geométrico-matemático a partir do qual toda arte deve se desenvolver:
Estou convencido de que é possível desenvolver uma nova forma de arte na qual o trabalho do artista poderia basear seu conteúdo num grau bastante substancial na linha de abordagem matemática (… ) O elemento de toda obra plástica é a geometria, relação de posições sobre o plano e no espaço” [ BILL]
Para o grupo Frente, a linguagem geométrica não era um ponto de chegada, mas sim um campo aberto à experiência e à indagação. Os artistas desse grupo pensavam a arte como um espaço em que a emoção deveria, necessariamente, emergir.
Lygia Clark trabalhou intensamente de acordo com os princípios do concretismo, mas não se acomodou. Ela passou a elaborar os postulados concretistas a partir de suas próprias inquietações.
Composição, 1953
Lygia pensava a arte não como obra acabada, “mas como estímulo à percepção, como proposta vivencial em busca da plenitude do ser, realizando-se no outro e através dele” [MILLIET].
Lygia, depois de explorar exaustivamente as possibilidades de composição que o espaço da tela delimitado pela moldura oferecia, caminha em direção a uma incorporação gradual da moldura à obra.
Composição nº 5 (1954)
Em Composição nº 5, da série Quebra da moldura, observe que a área tradicionalmente entendida como a área do quadro é verde e a área da moldura, preta, mas elas se interceptam. É como se a pintura transbordasse para além do seu limite e invadisse a moldura. Nessa obra a superfície se estende por igual da tela à moldura. Contudo, mesmo que de uma maneira diferente, a moldura ainda se impunha.
Lygia Clark avança na busca da desintegração da moldura. Ela abandona a tela e outros materiais tradicionais da pintura e passa a trabalhar com placas de madeira, tinta industrial, serra, maçarico e outros. Com as placas de madeira cortadas, a artista monta o retângulo da pintura. Não existe nem tela e nem moldura. O quadro é um todo, formado por placas de madeira compensada que a artista recorta, monta e cola em madeira Eucatex, como num jogo de quebra cabeça.
Superfície Modulada no. 9, de 1957.
O passo adiante em sua trajetória foi trabalhar com placas de metais, o que lhe possibilitou dar um grande salto. Nesse momento nasce a série Casulos- aqui o plano estufa e ganha tridimensionalidade, projetando-se em direção ao espaço exterior através de dobraduras.
Note que essas obras, apesar de inertes, dão a sensação de movimento, de vida. Elas se situam entre pintura e escultura, já que ainda se mantêm fixadas à parede.
Casulo, 1959. Nitrocelulose sobre lata
A referência aos organismos vivos será, a partir de agora, uma constante nessa nova etapa da trajetória de Lygia Clark.
Essa série demarca a fase neoconcreta da artista que busca a tridimensionalidade por entender que a arte deve se aproximar da vida das pessoas, deve ser uma arte vivida no espaço mesmo em que elas habitam.
O neoconcretismo (1959-61) visou a renovação da linguagem abstrata geométrica, em oposição ao caráter mecanicista e racionalista do concretismo. Propôs, a necessidade de se construir uma linguagem diretamente envolvida e relacionada com o sujeito humano para além das formas geométricas que seu olho possa captar, uma abordagem mais sensível e menos racional.
O neoconcretismo rejeitava assim qualquer movimento artístico que concebesse o processo criativo como uma tarefa mecânica, que limitasse a atividade artística a uma esfera elitista, e que transformasse as formas em fórmulas e na repetição de esquemas plásticos. Os artistas que participavam desse movimento estavam empenhados em construir uma arte vivencial, capaz de atender às expectativas de junção entre arte e vida.
“A arte não consiste mais em um objeto para você olhar, achar bonito, mas para uma preparação para a vida.” [CLARK]
Dos casulos nascem a famosa série Bichos. Essas obras saíram da parede e invadiram o espaço.
Quando o Casulo cai no chão vira Bicho. [GULLAR]
Bicho, 1960
“Bichos” são esculturas, feitas em alumínio, compostas de formas geométricas planas e com dobradiças, que promovem a articulação das diferentes partes que compõem o seu “corpo”, possibilitando infinitas posições quando manipulados. Como obra viva e orgânica, abertas a manipulação tornam-se passíveis à criação de diálogo com o participante.
Antes dos Bichos as obras de arte exigiam apenas o sentido da visão. Agora o tato, o toque das mãos, se torna necessário.
Essa série altera com a concepção tradicional de escultura, a qual o trabalho deveria nascer, obrigatoriamente, de um bloco maciço de algum tipo de pedra.
Em Bichos, Lygia Clark convida o espectador a ser coautor da obra. A obra só se completa na medida em que o espectador age sobre ela.
Tendo iniciado a produção destes objetos com triângulos e retângulos, aos poucos a artista acrescenta formas circulares e semicirculares a eles.
Com os Bichos, Lygia se torna a pioneira da arte participativa, e em 1961, ganha o prêmio de melhor escultura nacional na VI Bienal de São Paulo.
Com essa série, a artista inicia o processo de viver a arte ao invés de fazê-la.
Essas esculturas [bichos] são como uma árvore mágica, que dá esculturas como um pé de jaqueira dá jacas, um cajueiro, cajus. [PEDROSA]
Trepantes (1963)
Em seguida aos Bichos, cria os Trepantes (1963), recortes espiralados, feitos em metal, que podem surgir de uma caixa, enroscar-se em troncos ou em pequenos pedaços de madeira, como se fossem parasitas.
Os Trepantes feitos de borracha foram nomeados de “Obra Mole”.
Obra Mole (1964)
Neste mesmo ano, 1964, cria “Caminhando” obra que reforça a intenção de Lygia Clark se deslocar da posição de artista, inteiramente responsável pela criação de uma obra, para o de propositora. Aqui ela convida o espectador a cortar a famosa fita de Moebius [Descoberta em 1865 pelo matemático e astrônomo alemão August Ferdinand Moebius (1790-1868)], já utilizada anteriormente em “Unidade Tripartida, 1948-49”, de Max Bill, ícone da herança construtivista no Brasil.
Fita de Moebius
A noção de experiência na proposição Caminhando é ainda mais efetiva. Aqui uma fita de Moebius, em papel, é entregue a alguém com a proposta de que perfure sua superfície com uma tesoura e a corte longitudinalmente, trilhando o seu próprio caminho. A proposta feita não é apenas a vivência de uma experiência, mas a de dividir a criação desta obra com o espectador. O espectador torna-se então participador do processo criativo ao se relacionar com a obra.
“ […] Se eu utilizo ela uma fita de Moebius para esta experiência, é porque ela quebra os nossos hábitos espaciais. Ela nos faz viver a experiência de um tempo sem limite e de um espaço contínuo”
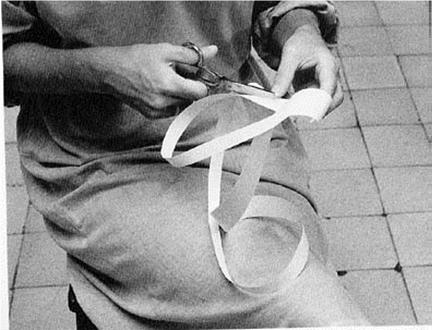
Caminhando.
Após Caminhando, Lygia cria seus últimos Bichos, que são também seus últimos objetos, para, em seguida, diluir sua arte no mundo – já entrando no campo da arte-terapia.
A grande aventura sensorial proposta por Lygia Clark começou com “Livro Sensorial”, de 1966, que não tinha textos, mas uma coleção de volumes, como conchas, novelos de lã e pedras, guardadas em páginas de plástico transparente, para serem experimentados pelo toque.
A partir de 1966/67, Lygia começa a produzir objetos criados especialmente para explorar e estimular o corpo.
Começando pela série “Natureza – estrutura cega” em que ela começa a excluir a visão para privilegiar os outros sentidos, vai chegar à série “Nostalgia do corpo”, na qual cada um dos sentidos vai ser explorado através de objetos que são criados para estimular, primeiramente novas percepções e gradativamente a sensação, mais além da percepção e do sentimento.
Retorna a Paris por volta de 1968 com uma bolsa na Sorbonne e em 1972 é convidada a ministrar um curso sobre comunicação gestual na universidade e por lá permanece por 8 anos.
Livro Sensorial
Em 1976, Lygia Clark volta definitivamente ao Rio de Janeiro. Abandona, então, as experiências com grupos e inicia uma nova fase com fins terapêuticos.
Em 1981, Lygia diminui paulatinamente o ritmo de suas atividades. Em 1983 é publicado, numa edição limitada de 24 exemplares, o “Livro Obra”, uma verdadeira obra aberta que acompanha, por meio de textos escritos pela própria artista e de estruturas manipuláveis, a trajetória da obra de Lygia desde as suas primeiras criações até o final de sua fase neoconcreta. Em abril de 1988, Lygia Clark falece.
Leia mais: Por que o modelo educacional não será mais o mesmo depois da covid-19
Atividades com as obras de Lygia Clark
Muitas foram as atividades desenvolvidas a partir da obra dessa genial artista.
Construímos com os alunos diferentes Bichos e o manipulamos. Criamos também a famosa Faixa de Mobius. Descobrirmos que ela é uma superfície especial pois é unilateral, só tem um lado. Ao percorre-la, observamos um caminho sem início nem fim, infinito e com ela, vivenciamos a proposição Caminhando.
Planos em superfície modulada
Para conhecer um pouco mais sobre essas obras assista a dois vídeos gravados na exposição Lygia Clark: uma retrospectiva que ocorreu em 2012, no Itaú Cultural. No primeiro, pessoas interagem e experimentam formas com réplicas de Bichos e no segundo, uma participante vivencia a proposição Caminhando.
https://www.youtube.com/watch?v=lfitsC4m_dY
https://www.youtube.com/watch?v=3sP-uT5DQLM
Com obras da série Planos em superfície modulada exploramos a simetria de rotação; e propomos aos alunos que, inspirados nelas, criassem a sua obra utilizando esse mesmo tipo de simetria.
Com a obra Plano em superfície moduladas nº2 realizamos muitas propostas, entre elas:
Plano em superfície moduladas nº2 ( 1956)
1- A obra é formada somente por quadriláteros. Que quadriláteros que você identifica na obra?
2- Determine a medida dos ângulos de cada uma das figuras que aparecem nesse quadro.
3- Reproduza a obra, utilizando material de desenho. Recorte cada quadrilátero que a compõem, obtendo assim um quebra-cabeça com 14 peças. Quantos eixos de simetria têm cada uma dessas peças?
Agora,
- a) Monte:
- Com 2 dessas figuras, um quadrado.
- Com 2 dessas figuras, um paralelogramo.
- Com 2 dessas figuras, um trapézio isósceles.
- Com 2 dessas figuras, um trapézio retângulo.
- Com 3 dessas figuras, um retângulo.
- Com 3 dessas figuras, um trapézio.
b) Crie outros dois desafios diferentes dos propostos anteriormente.
4- Note que a área ocupada por dois retângulos que aparecem nesse quadro é igual a área de um dos paralelogramos amarelos do quadro. Utilizando recortes, mostre esse fato.
5- Calcule a área e o perímetro do quadro.
6-Faça cópias do quadro. Agora, utilize as cópias para pintar de três maneiras diferentes 1/2 do quadro.
Para conhecer um pouco mais sobre esta brilhante artista e sobre outras atividades realizadas em minha pesquisa envolvendo Matemática e Arte, assista aos vídeos:
http://www.youtube.com/watch?v=LNH55z0dsO4
https://www.youtube.com/watch?v=67KZUV1xzfM
No primeiro, Felipe Scovino, um dos curadores da exposição Lygia Clark: uma retrospectiva de 2012, Itaú Cultural -SP, explora o desenvolvimento da obra da artista em direção a obras mais participativas, que chamam à interação, ao estímulo dos sentidos, às relações Interpessoais.
No segundo, Alessandra Clark, coordenadora de projetos especiais da Associação Lygia Clark e neta da artista, expõe conceitos fundamentais da trajetória de Lygia a partir de obras presentes nessa mesma exposição.
E conheça os livros Tecendo matemática com arte e Fazendo arte com a matemática, ambos escritos por mim em parceria com a doutora Estela Kaufman Fainguelernt.
Para concluir cito o crítico Mário Pedrosa, autor de uma das mais precisas definições da obra de Lygia Clark: “É um exercício experimental da liberdade”.
Sobre a autora
Katia Regina Ashton Nunes é Mestre em Educação Matemática, Coordenadora de Matemática da Educação Infantil ao Ensino Médio da Associação Educacional Miraflores- Niterói- RJ, e autora de artigos e dos livros Fazendo arte com a matemática, Tecendo matemática com arte, Descobrindo matemática na arte e Matemática: práticas pedagógicas para o ensino médio, todos da editora Artmed/Penso. Seu e-mail é katiaanunes@hotmail.com.
REFERÊNCIAS BIBLIOGRAFICAS:
CARVALHO, Dirce H. B. de; LEFÈVRE, José Eduardo. Lygia Clark: o vôo para o espaço real – do bi para o tridimensional. USP, São Paulo, 2008.
FAINGUELERNT, Estela K; NUNES, Katia R.A .Tecendo matemática com arte. Porto Alegre: Artmed, 2009.
________________________________________.Descobrindo matemática na arte. Porto Alegre: Artmed, 2010.
_____________________________________. Matemática: práticas pedagógicas para o ensino médio. Porto Alegre: Penso, 2012.
_____________________________________. Fazendo arte com a matemática. 2 ed. Porto Alegre: Penso, 2015.
MEDEIROS, Izabella Maria S. O projeto da arte-vida de Lygia Clark: rupturas e desafios na formulação de um projeto de arte contemporânea. UFP, Pernambuco, 2012.
MILLIET, Maria Alice. Lygia Clark: Obra-trajeto. São Paulo: Editora da Universidade de São Paulo, 1992.
MORAN, José. Desafios na comunicação pessoal. 3ed. São Paulo: Paulinas, 2007.
RICKEY, George. Construtivismo – origens e evolução. São Paulo: Cosac & Naify, 2002, p. 60.
Comments